The Algorithm Design Manual (3rd) Exercise Solution 'E2-32'

Table of Contents

• Introduction
• Repository
• Exercise 2-32
  • Question
  • Solution
    • Solution for (a)
    • Solution for (b)
    • Solution for (c)
    • Solution for (d)

Introduction

This series is my solutions for algorithm exercises in'The Algorithm Design Manual' 3rd edition.
It's my solutions, not model answers, so if you find some mistakes or more sophisticated solutions, please post in comment area below.

Repository

Here

Exercise 2-32

Question

For each of the following expressions $f(n)$ find a simple $g(n)$ such that $f(n) = Θ(g(n))$.

$$\begin{align*} \text{(a)}\quad&f(n)=\sum_{i=1}^n\frac{1}{i}\\ \text{(b)}\quad&f(n)=\sum_{i=1}^n\left\lceil\frac{1}{i}\right\rceil\\ \text{(c)}\quad&f(n)=\sum_{i=1}^n\log{i}\\ \text{(d)}\quad&f(n)=\log{n!} \end{align*}$$

Solution

Solution for (a)

As a graph below shows, the summation can be regarded as an uppersum of a function $y=\frac{1}{x}$ and bound by two reciprocal functions.

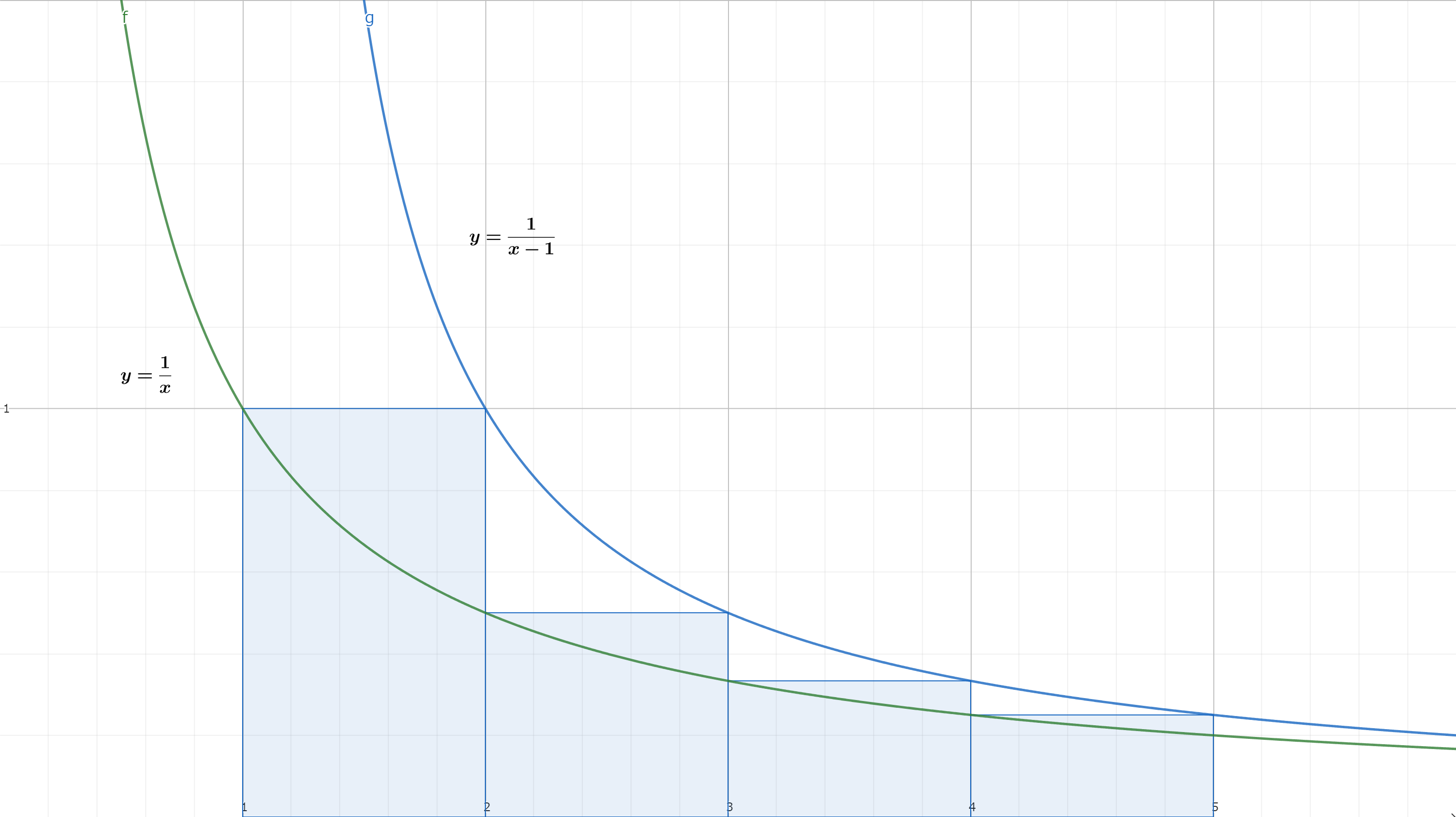
And the next inequation holds:

$$\begin{equation} \int_1^n\frac{1}{x}dx \le \sum_{i=1}^n\frac{1}{i} \le \int_2^{n+1}\frac{1}{x-1}dx+1 \end{equation}$$

Think of solving Left Hand Side and Right hand Side of the above formula.

$$\begin{align} \int_1^n\frac{1}{x}dx &= \left[\ln{|x|}\right]_1^n\\ &=\ln{n} \end{align}$$ $$\begin{align} \int_2^{n+1}\frac{1}{x-1}dx+1 &= \left[\ln{|x-1|}\right]_2^{n+1}+1\\ &=\ln{n}+1 \end{align}$$

So, $f(n)$'s boundation and function $g(n)$ is:

$$\begin{equation} f(n)=\Theta(\log{n}) \end{equation}$$ $$\begin{equation} g(n)=\log{n} \end{equation}$$

Solution for (b)

$$\begin{equation} o \lt \frac{1}{i} \lt 1 \quad \text{for} \{i\in\mathbb{N}\} \end{equation}$$

So,

$$\begin{align} \left\lceil \frac{1}{i} \right\rceil&=1\\ f(n)&=\sum_{i=1}^n\left\lceil\frac{1}{i}\right\rceil=n \end{align}$$

So function $g(n)$ is:

$$\begin{equation} g(n)=n \end{equation}$$

Solution for (c)

From similar analysis as promlem(a),

$$\begin{equation} \int_1^n\log{x}dx \lt \sum_{i=1}^n\log{i} \lt \int_2^{n+1}\log{(x-1)}dx+1 \end{equation}$$

Think of LHS and RHS.
For simplicity, we think abount $\ln{x}$ rather than $\log{x}$(the asymptotical order is same).

$$\begin{align} LHS&=\int_1^n\ln{x}dx\\ &=\left[x\ln{x}\right]_1^n-\int_1^n1dx\\ &=n\ln{n}+\Theta(n)\\ &=\Theta(n\log{n}) \end{align}$$ $$\begin{align} RHS&=\int_2^{n+1}\ln{(x-1)}dx+1\\ &=\left[x\ln{(x-1)}\right]_2^{n+1}-\int_2^{n+1}(1-\frac{1}{n-1})dx+1\\ &=\Theta(n\ln{n})+\Theta(n)+\Theta(\ln{n})+\Theta(1)\\ &=\Theta(n\log{n}) \end{align}$$

So,

$$\begin{equation} g(n)=n\log{n} \end{equation}$$

Solution for (d)

The product as an anti-logarithm can be distributed into the summation of logarithm.

$$\begin{align} f(n)&=\log{n!}\\ &=\sum_{i=1}^n\log{i} \end{align}$$

The shape of the formula is exactly the same as that in the problem (c).
So the result is also the same.